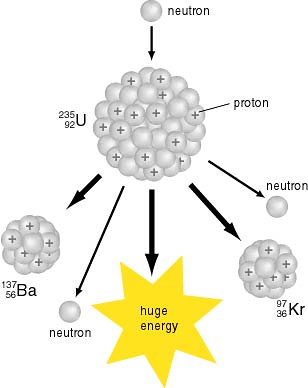
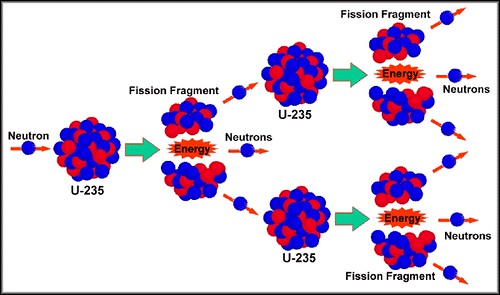
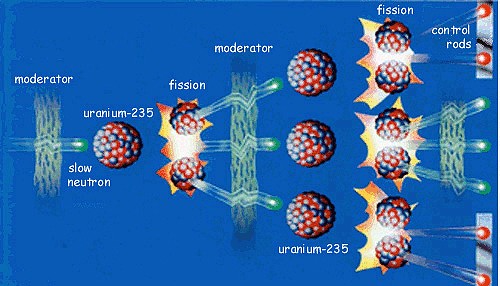
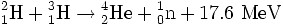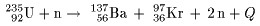先简å•ä»‹ç»ä¸€ä¸‹”放射性”,”è¾å°„”这些东西是怎么回事。
ä¸€ä¸ªäººæœ¬è´¨ä¸Šå°±æ˜¯ä¸€å †åŽŸå,这些原å通过å„自电å和质å的互相å¸å¼•æŽ’æ–¥ 交å‰ç»“åˆå½¢æˆåˆ†å,DNAç‰ç‰ã€‚如果有一个外æ¥ç²’å,比如说一个高速电å或者光å打过æ¥ï¼Œå®ƒå¯èƒ½æŠŠè¿™å †è¿è¡Œè‰¯å¥½çš„原å机器上的æŸä¸ªåŽŸå的电å打飞,导致这 个原å电离,就会改å˜å®ƒçš„带电é‡ï¼Œä½¿å®ƒè·Ÿå…¶ä»–原å的相互æé…出现å差:
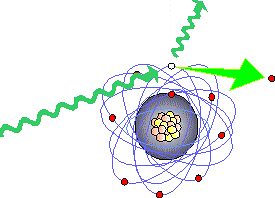
如果很多原å都这么被外æ¥ç²’åé€ æˆç”µç¦»ï¼Œæœ€åŽå¿…然打乱分åå’ŒDNA的排列组åˆï¼Œäººä½“ç»„ç»‡å°±ç ´å了。DNA/RNA 乱了就会å‘生”å˜å¼‚”。当然也å¯èƒ½ä¼šå‘生好的å˜å¼‚(比如把黄瓜ç§åé€ä¸Šå¤ªç©ºå›žæ¥å˜æˆè¶…级蔬èœï¼‰ï¼Œä½†å¤§å¤šæ•°æƒ…况下ä¸å¤ªå¥½ï¼Œé‡çš„甚至是直接æ»äº¡ï¼Œè½»çš„也å¯èƒ½ä¼š ä¼ ç»™ä¸‹ä¸€ä»£ã€‚
è¿™ç§æŠŠåŽŸå打电离的行为被称为”致电离è¾å°„”,å¯ä»¥æƒ³è§ï¼Œè¿™ç§è¾å°„需è¦é«˜é€Ÿï¼Œä¹Ÿå°±æ˜¯é«˜èƒ½é‡çš„带电粒å或者光å。很多人谈论”手机è¾å°„”,或者计算机显示器的”è¾å°„”,那些都是éžç”µç¦»è¾å°„,至今没有直接è¯æ®è¡¨æ˜Žæ‰‹æœºäº§ç”Ÿçš„那么一点点能é‡å¯¹äººä½“真æ£æœ‰å®³ã€‚
其实生活ä¸æ¯ä¸ªäººæ¯æ—¶æ¯åˆ»éƒ½åœ¨æŽ¥å—æ¥è‡ªå®‡å®™å°„线的电离è¾å°„。这些宇宙射线就是高速带电粒åï¼Œç”¨ä¸€ä¸ªç›–æ ¼è®¡æ•°å™¨å¯ä»¥å¾ˆå®¹æ˜“的探测到。好在我们å—到的è¾å°„很 少。地çƒå¤–层空间有大é‡çš„高速带电粒å,多äºåœ°ç£åœºå’Œå¤§æ°”层的ä¿æŠ¤ï¼Œç»å¤§å¤šæ•°åˆ°ä¸äº†åœ°é¢ã€‚这就是为什么è¦æŠŠç§åé€åˆ°å¤ªç©ºåŽ»æŽ¥å—è¾å°„。对于宇航员æ¥è¯´ï¼Œè¾å°„ 是个严é‡é—®é¢˜ï¼Œè‡³ä»Šæ²¡æœ‰ä»€ä¹ˆå¥½çš„办法æ¥é˜²æŠ¤ã€‚地çƒç£åœºçš„尺度比地çƒåŠå¾„å¤§å¾—å¤šå¾—å¤šï¼Œå› æ¤ç©ºé—´ç«™ä¸Šçš„宇航员呆一两年å—到è¾å°„也å¯ä»¥å¿å—。但如果去ç«æ˜Ÿçš„è¯ï¼Œ å—到的è¾å°„剂é‡æ˜¯ç›¸å½“大的。大约两年å‰çœ‹çº½çº¦æ—¶æŠ¥çš„报é“,ç«æ˜Ÿç™»é™†è®¡åˆ’的一个é‡è¦éš¾ç‚¹å°±æ˜¯æ€Žä¹ˆé˜²æŠ¤å®‡å®™å°„线的è¾å°„,这个难å¯èƒ½ç‚¹è¿˜æ²¡æœ‰è§£å†³ã€‚
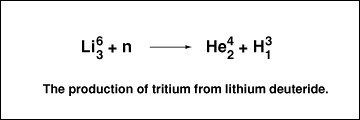
地é¢ä¸Šçš„高速带电粒å都是æ¥è‡ªæ”¾å°„性衰å˜æˆ–è€…æ ¸å应,或者粒ååŠ é€Ÿå™¨ã€‚è¯´ä¸€ç§ç‰©è´¨å…·æœ‰æ”¾å°„性,æ„æ€å°±æ˜¯è¯´æŠŠå®ƒæ”¾åœ¨é‚£é‡Œå®ƒè‡ªå·±å°±ä¼šå¾€å¤–å‘射高速带电粒å, 比如说氦离å(α衰å˜ï¼‰ï¼Œç”µå(β衰å˜ï¼‰ï¼Œæˆ–者光å(γ衰å˜ï¼‰ã€‚这就是为什么说放射性是一ç§æ±¡æŸ“。裂å˜ååº”å †å应出æ¥çš„副产å“往往具有放射性,必须把它们 妥善ä¿ç®¡è¿œç¦»äººç¾¤ï¼Œç§°ä¸ºæ ¸åºŸæ–™ã€‚
相比之下èšå˜å应的废料是氦4å’Œä¸å。氦4很好,就是气çƒé‡Œé‚£ç§æ°”体。但ä¸å就很有问题了。ä¸å ä¸å¸¦ç”µï¼Œä»Žè¿™ä¸ªè§’度它ä¸å¯èƒ½ç›´æŽ¥å¯¼è‡´è‡´ç”µç¦»è¾å°„。但æ£å› 为ä¸åä¸å¸¦ç”µï¼Œå®ƒå¾ˆå®¹æ˜“直接接触原åæ ¸ï¼Œå¯¼è‡´äººä½“å†…åˆ†åæ–裂。ä¸å弹就是用这个原ç†ï¼Œå·ç§°åªæ€äººä¸ 拆房å。但由于ä¸åå¯ä»¥ç”¨é‡æ°´æˆ–者石墨之类的东西æ¥é˜²æŠ¤ï¼Œå®ƒçš„”直接伤害”并ä¸å¤§ã€‚
èšå˜å应ä¸å的真æ£éº»çƒ¦ä¹‹å¤„在于ä¸åå¯ä»¥è·Ÿå 应装置的墙å£å‘ç”Ÿæ ¸å应。用一段时间之åŽï¼ˆæ ¹æ®ä¸€æœ¬è®²ä¸»æµèšå˜çš„书是三五åå¹´ï¼Œæ ¹æ®ä¸€ç¯‡è®²æ°¦3çš„æ–‡ç« æ˜¯åæ¥å¹´ï¼‰å°±å¿…须更æ¢ï¼Œå¾ˆè´¹é’±ã€‚而且æ¢ä¸‹æ¥çš„墙å£å¯èƒ½ 有放射性(å–决于墙å£æ料的选择),æˆäº†æ ¸åºŸæ–™ã€‚还有一个ä¸å¥½çš„å› ç´ æ˜¯æ°šå…·æœ‰æ”¾å°„æ€§ï¼Œè€Œä¸”æ°šä¹Ÿå¯èƒ½è·Ÿå¢™å£å应。
å› ä¸ºè¿™ä¸ªåŽŸå› ï¼Œæœ‰äººè®¤ä¸ºæ°˜æ°šèšå˜åªèƒ½ç®—”第一代”èšå˜ï¼Œä¼˜ç‚¹æ˜¯ç‡ƒæ–™æ— 比便宜,缺点是有ä¸å。
“第二代”èšå˜æ˜¯æ°˜å’Œæ°¦3å应。这个å应本身ä¸äº§ç”Ÿä¸å,但其ä¸æ—¢ç„¶æœ‰æ°˜ï¼Œæ°˜æ°˜å应也会产生ä¸å,å¯æ˜¯æ€»é‡éžå¸¸éžå¸¸å°‘。如果第一代电站必须远离闹市区,第二代估计å¯ä»¥ç›´æŽ¥æ”¾åœ¨å¸‚ä¸å¿ƒã€‚
“第三代”èšå˜æ˜¯è®©æ°¦3è·Ÿæ°¦3å应。这ç§èšå˜å®Œå…¨ä¸ä¼šäº§ç”Ÿä¸å。但æ£å¦‚有人指出的,åªè¦æ˜¯æ ¸å应就ä¸èƒ½è¯´ç»å¯¹æ²¡æœ‰æ±¡æŸ“ï¼Œå…·ä½“æ€Žä¹ˆæ ·å¿…é¡»è®©å®žè·µå›žç”。ç†è®º 上讲,第三代ååº”å †å¯ä»¥ç›´æŽ¥æ”¾åœ¨å®‡å®™é£žèˆ¹ä¸Šäº†ã€‚这个ååº”å ªç§°ç»ˆæžèšå˜ï¼Œå°±å¥½åƒã€Šå˜å½¢é‡‘åˆšã€‹ä¸€æ ·ï¼Œåªéœ€è¦æ”¶é›†ä¸€ç§”能é‡å—”,ä¸ç”¨è€ƒè™‘è¥å…»æé…。虽然地çƒä¸Š 没有,但月çƒï¼Œæœ¨æ˜Ÿï¼ŒåœŸæ˜Ÿä¸Šéƒ½å¤šå¾—是,用ä¸ç€æŠ¢ã€‚
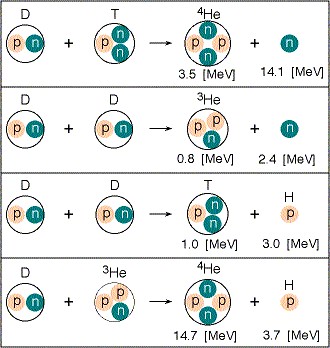
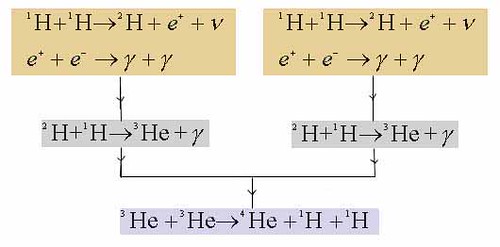
第二代和第三代èšå˜å应的方程:
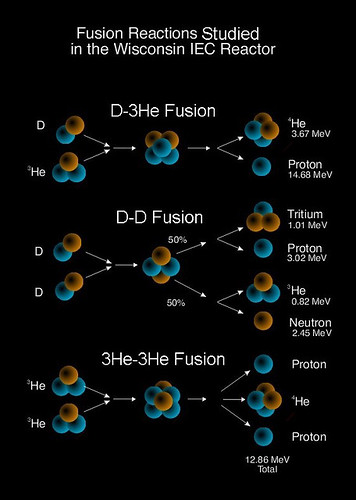
飞船上用氦3çš„å¦ä¸€ä¸ªå¥½å¤„是产生的å应物都是带电粒å,å¯ä»¥ç”¨ç”µç£åœºçš„方法å‘外喷射直接当å‘åŠ¨æœºã€‚å¦‚æžœæ˜¯ä¸€å¤§å †ä¸å就很难控制了。但尽管如æ¤ï¼Œå¾ˆå¤šèšå˜å‘动机的设想ä»ç„¶æ˜¯ä½¿ç”¨æ›´å®¹æ˜“实现的氘氚èšå˜ï¼ˆå–·å°„α粒å),比如下é¢è¿™ä¸ªï¼š
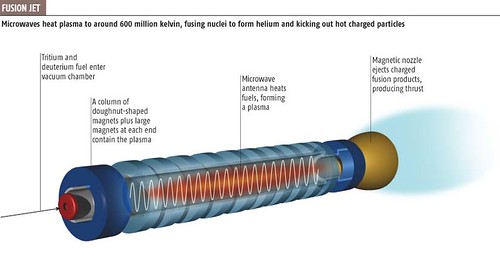
如果用氘和氦3èšå˜çš„è¯ï¼Œå› 为产生的质å也带电å¯ä»¥ç”¨æ¥å¾€å¤–喷射,显然效率会大大æ高。èšå˜å‘动机的最大优势在于燃料é‡é‡å¾ˆè½»ï¼Œå¯ä»¥å¤§å¤§ç¼©çŸèˆªè¡Œæ—¶é—´ã€‚
所以如果人类已ç»æ˜¯å·§å¦‡ä»€ä¹ˆé¥éƒ½ä¼šåšï¼Œæ°¦3è¿™ç§ç±³æ˜¾ç„¶å‘³é“最好。
问题是,如果现在我们连第一代èšå˜éƒ½ä¸ä¼šåšï¼Œä¸ºä»€ä¹ˆè¿˜æœ‰è¿™ä¹ˆå¤šäººè°ˆè®ºæ°¦3å‘¢ï¼Ÿæ ¹æ®æ‹‰å§†æ–¯è²å°”德的分类法,美国在åæ战争ä¸é¢ä¸´çš„困难包括 “已知的已知”,”已知的未知”,和”未知的未知”。我们å‰é¢æ‰€è®²çš„所有东西都是”已知的已知”。下é¢è¦ä»‹ç»çš„将是”已知的未知”了,è¯é¢˜å¾ˆå¯èƒ½ä¼šå¼•èµ·äº‰ 议。
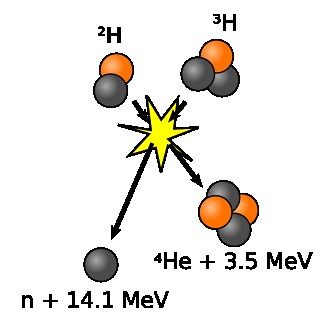
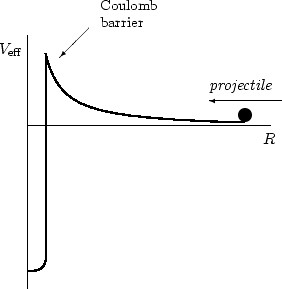
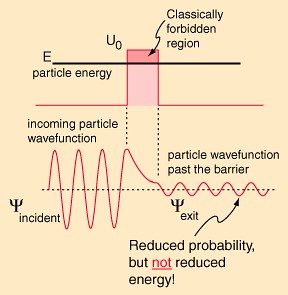
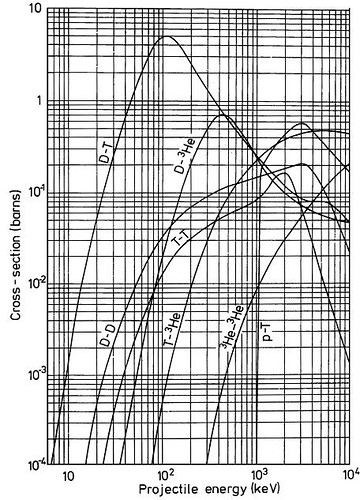
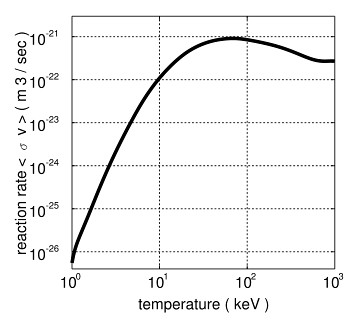
对于å—æŽ§æ ¸èšå˜æ¥è¯´ï¼Œæ¸©åº¦æ˜¯æœ€å…³é”®çš„。氘氚èšå˜éœ€è¦çš„温度是10KeV (相当于1亿度),而氘与氦3çš„èšå˜ï¼Œè¦æƒ³è¾¾åˆ°ä¸€ä¸ª”体é¢çš„”å应率,需è¦çš„温度是100KeV。达到这个温度并ä¸éš¾ï¼Œæ¯”如日本的JT-60å·²ç»å®žçŽ°äº† 50KeV。å¯æ˜¯æ¸©åº¦è¶Šé«˜ï¼Œä¿æŒè¿™ä¸ªæ¸©åº¦ä¹Ÿè¶Šå›°éš¾ã€‚从这个角度推测,氦3èšå˜å¿…然比氘氚èšå˜è¦å›°éš¾ã€‚既然如æ¤ä¸ºä»€ä¹ˆæœ‰è¿™ä¹ˆå¤šäººè°ˆè®ºæ°¦3,难é“他们都是å°å¦ 还没毕业就设计åšå£«è®ºæ–‡ä¹ˆï¼Ÿ
在一本1997年出版的书里é¢ï¼Œä»¥åŠåœ¨ç½‘上æœç´¢æ°¦3èšå˜ï¼Œæ‰€æœ‰é“¾æŽ¥éƒ½æœ€ç»ˆæŒ‡å‘å¨æ–¯åº·æ˜Ÿå¤§å¦çš„èšå˜æŠ€æœ¯ å¦é™¢ä¸çš„一个实验室。这个实验室实现了氦3çš„èšå˜å应。更有æ„æ€çš„是,他们用的办法ä¸æ˜¯ä¸»æµçš„托克马克或者惯性约æŸï¼Œè€Œæ˜¯”é™ç”µåœºçº¦æŸ” (Inertial-Electrostatic-Confinement,以下简称IEC)。这其实是一个已ç»æœ‰å‡ å年历å²çš„设计(也å«fusor), 其原ç†å¦‚下图:
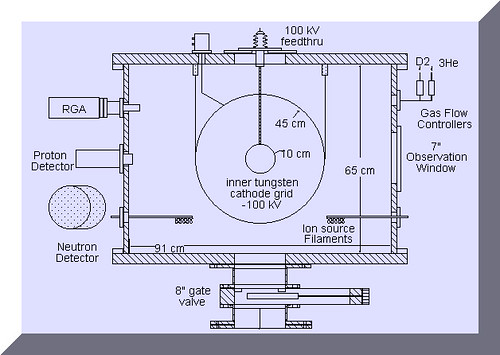
图ä¸åŠå¾„45厘米的大çƒæ˜¯ä¸€ä¸ªçœŸç©ºå®¤ï¼Œé‡Œé¢æœ‰ä¸€ä¸ªåŠå¾„10åŽ˜ç±³çš„é‡‘å±žç½‘æ ¼ã€‚çœŸç©ºå®¤çš„ç”µåŽ‹ä¸º0ï¼Œè€Œé‡‘å±žç½‘æ ¼å¸¦æœ‰10万ä¼çš„è´Ÿé«˜åŽ‹ï¼Œè¿™æ ·å°±å½¢æˆäº†ä¸€ä¸ªç”µåœºã€‚ å› ä¸ºå‚与èšå˜å应的原料都是带æ£ç”µçš„离å,它们一定在电场作用下会以高速往ä¸é—´è·‘,并且æ¥å›žéœ‡è¡ï¼Œåœ¨ç¢°æ’žè¿‡ç¨‹ä¸å°±ä¼šå‘生èšå˜å应。相对于ITERé‚£æ ·çš„åºž 然大物,IEC整个装置并ä¸æ˜¯å¾ˆå¤§ï¼ˆè¿™å“¥ä»¬ä¸ä¼šæ‰¾æˆ‘è¦è‚–åƒæƒå§ï¼‰ï¼š

å†…éƒ¨çš„é‡‘å±žç½‘æ ¼é—ªé—ªå‘光:

在这个装置上已ç»å®žçŽ°äº†ç¨³å®šçš„æ°˜-æ°¦3èšå˜ï¼Œå应率达到了æ¯ç§’260万次,产生了大é‡è´¨å,但输出能é‡è¿œå°äºŽè¾“入能é‡ï¼Œç›®å‰è¿˜è¿œè¿œä¸è¶³ä»¥ç”¨æ¥å‘ç”µã€‚ç›®å‰ IEC的实用价值主è¦æ˜¯å¯ä»¥ä½œä¸ºä¸€ä¸ªä¾¿æºå¼çš„ä¸åå’Œæ£ç”µå产生器,比如说用于医å¦ã€‚我本能的å应是,这ç§æœ‰ç‚¹å¦ç±»çš„装置是å¦èƒ½ç‹¬è¾Ÿè¹Šå¾„?具体说,就是:
“é™ç”µåœºçº¦æŸ”+æ°¦3,在技术上是å¦æ¯”主æµ+氘氚,更有å¯èƒ½æ—©æ—¥å®žçŽ°èšå˜å‘电?
æœ‰è°ƒæŸ¥ç ”ç©¶æ‰æœ‰å‘言æƒã€‚åœ¨ç½‘ä¸Šæ ¹æœ¬æœç´¢ä¸åˆ°ä¸Šé¢è¿™ä¸ªé—®é¢˜çš„ç”案。所以我åšçš„è°ƒæŸ¥ç ”ç©¶éžå¸¸ç®€å•ã€‚我直接给这个实验室å‘了å°ç”µå邮件。
我æ出了两个问题:1)对于氦3èšå˜æ¥è¯´ï¼ŒIEC是å¦æ˜¯æ¯”主æµè£…置更有优势?2)对于IECæ¥è¯´ï¼Œç›¸å¯¹äºŽä¸»æµçš„氘氚èšå˜ï¼Œå®ƒæ˜¯å¦æ›´æ„¿æ„进行氦3èšå˜ï¼Ÿ
回信éžå¸¸å®žåœ¨ï¼š1)主æµä¸åšæ°¦3ï¼Œæ˜¯å› ä¸ºä¸»æµè£…置都是专门设计的大型装置,当然è¦åšæ›´çŽ°å®žçš„氘氚èšå˜ï¼›2)å³ä½¿æ˜¯å¯¹äºŽIECæ¥è¯´ï¼Œä¹Ÿæ˜¯æ°˜æ°šèšå˜æ›´å®¹æ˜“。 对于氦3ï¼Œå› ä¸ºå®ƒæœ‰ä¸¤ä¸ªè´¨å,所以如果能把氦3原å的两个电å都打掉,它的带电é‡å°±æ¯”氘氚高一å€ï¼Œä»Žè¿™ä¸ªè§’度æ¥è¯´çš„确在IEC里é¢æ›´å®¹æ˜“åŠ é€Ÿã€‚ä½†ä»–æ‰¿è®¤ï¼Œ ç›®å‰è¿˜ä¸çŸ¥é“怎么打掉第二个电å。
在回信ä¸è¿™ä¸ªå“¥ä»¬è¿˜å‘Šè¯‰æˆ‘一个我在网上没看到的情况,就是è¦æƒ³å¢žåŠ å应率,必须æ高能é‡è¾“入,但å应率似乎有一个上é™ï¼ŒæŽ¥è¿‘这个上é™çš„æ—¶å€™ä½ å¢žåŠ å¾ˆå¤šå¾ˆå¤šèƒ½é‡ï¼Œå应率å´åªå¢žåŠ 一点点。
åŽæ¥æˆ‘在wikipedia介ç»fusorçš„æ¡ç›®ä¸æŸ¥åˆ°äº†å…¶ä¸çš„æœ¬è´¨åŽŸå› ã€‚é™ç”µåœºçº¦æŸåªèƒ½çº¦æŸå¸¦æ£ç”µçš„离å(ä¸å¿ƒç½‘æ ¼å¸¦è´Ÿç”µï¼‰ï¼Œæˆ–è€…åªèƒ½çº¦æŸç”µå(ä¸å¿ƒ ç½‘æ ¼å¸¦æ£ç”µï¼‰ï¼Œä½†ä¸èƒ½åŒæ—¶çº¦æŸç¦»å和电å。IEC的情况是真空室里é¢èƒ½è¾¾åˆ°ä¸å¿ƒçš„åªèƒ½æ˜¯ç¦»å,而这么多离åèšåœ¨ä¸€èµ·ä»–们会互相排斥,也就是说密度高ä¸äº†ã€‚ 这也就æ„味ç€å应出æ¥çš„能é‡å¯†åº¦é«˜ä¸äº†ã€‚而托克马克里é¢æ˜¯åŒæ—¶æœ‰ç”µå和离å的,åªä¸è¿‡ä»–们互相自由è¿åŠ¨è€Œå·²ï¼Œæ‰€ä»¥æ‰˜å…‹é©¬å…‹å¯ä»¥è¾¾åˆ°ç›¸å¯¹æ¯”较高的密度。æ£æ˜¯ å› ä¸ºè¿™ä¸ªåŽŸå› ï¼Œæœ‰äººè®¤ä¸ºIEC装置永远也ä¸å¯èƒ½å®žçŽ°èšå˜å‘电。
其实还有一些其他的装置å¯ä»¥å®žçŽ°æ°¦3èšå˜ï¼Œä½†ç›®å‰ä¸ºæ¢æ°¦3èšå˜çš„”主浔是IEC。然而IEC是èšå˜å‘电的”éžä¸»æµ”,它固然有很多具体应用,å¯æ˜¯å‘电看æ¥å¸Œæœ›æ¸ºèŒ«ã€‚除éžå°†æ¥å‘现”未知的未知”,å¦åˆ™æ°¦3必然是一个比氘氚还è¦é¥è¿œçš„梦想。
所以我å‘现的ç”æ¡ˆæ˜¯è¿™æ ·çš„ï¼šä¸ºä»€ä¹ˆè¿™ä¹ˆå¤šäººè°ˆè®ºæ°¦3ï¼Ÿå› ä¸ºç§‘å¦å®¶éœ€è¦å‘表论文。我曾ç»çœ‹åˆ°ä¸€ä¸ªéžå¸¸é•¿çš„å®£ä¼ æ°¦3的演示文件,å‰é¢ç›¸å½“大的篇幅居然是从能æºå±æœºå¼€å§‹è°ˆï¼Œåˆ°æœ€åŽä¹Ÿæ²¡è¯´å¤šå°‘技术å¯è¡Œæ€§ã€‚æ°¦3的确很é¥è¿œï¼Œä½†NASA有ä¸å°‘ç»è´¹æ”¯æŒèšå˜å‘动机。
登月需è¦ç†ç”±ä¹ˆï¼Ÿä»…仅带动一个国家相关å¦ç§‘å‘展这一æ¡ï¼Œå®ƒå°±ä¸å¯èƒ½æ˜¯å½¢è±¡å·¥ç¨‹ã€‚所以我认为登月就好好登月,没必è¦éžå¾—说氦3。…